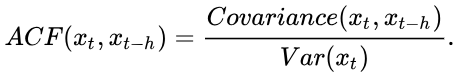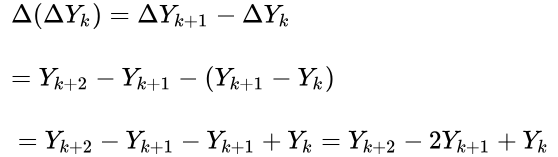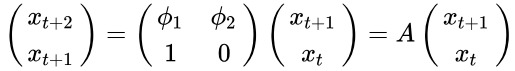ARIMA（Autoregressive Integrated Moving Average Model）

目录

1 相关概念

1.1 平稳性

1.2 时间序列的弱平稳性

1.3 差分法

1.3.1 概念

1.3.2 差分的性质

1.3.3 差分方程的概念

1.4 问题定义

2 自回归模型（Autoregressive Model，AR）

2.1 AR 模型的引入

2.2 AR(1) 模型

2.3 AR(p) 模型

3 滑动平均模型 MA

4 ARMA

4.1 基本原理

4.2 基本形式 

5 差分技巧 Integrated

6 ARIMA

7 季节性 Seasonal ARIMA

8 ARIMA模型注意点

8.1 ARIMA的优缺点

8.2 判断是时序数据是稳定的方法

8.3 ARIMA的参数与数学形式

 8.4 ARIMA的建模

8.5 ACF(autocorrelation function)和偏自相关函数PACF(partial autocorrelation function)

        对时间序列数据进行分析和预测比较完善和精确的算法是博克思-詹金斯(Box-Jenkins)方法，其常用模型包括：自回归模型（AR模型）、滑动平均模型（MA模型）、（自回归-滑动平均混合模型）ARMA模型、（差分整合移动平均自回归模型）ARIMA模型。

        ARIMA模型（英语：Autoregressive Integrated Moving Average model），差分整合移动平均自回归模型，又称整合移动平均自回归模型（移动也可称作滑动），是时间序列预测分析方法之一。ARIMA(p，d，q)中，AR是“自回归”，p为自回归项数；MA为“滑动平均”，q为滑动平均项数，d为使之成为平稳序列所做的差分次数（阶数）。“差分”一词虽未出现在ARIMA的英文名称中，却是关键步骤。

        方差越大，数据波动越大，方差计算公式如下式所示：

        方差等于1，那么标准差也就是1，表示概率函数在对称轴左右偏差1的位置导数为0，即为拐点。期望为0，表示概率函数以y轴为对称轴。

        平稳性分为严平稳和弱平稳：

        那么如果我们拿到的数据波动很大，那么需要平稳这个数据，如何平稳这个数据呢？

        要讲解自回归模型，就必须提到时间序列的弱平稳性。一个时间序列  具有弱平稳性（Weak Stationary）指的是：

       另外，时间序列的自相关方程（AutoCorrelation Function）指的是对于  可以定义 ACF 为

        如果时间序列  在弱平稳性的假定下，ACF 将会简化为

        差分方程：差分方程 - 知乎

        n阶常系数齐次线性差分方程解的结构：n阶常系数齐次线性差分方程解的结构 - 豆丁网

        设函数 f(x) 在下面数列上有定义，则对应的函数的值为：

        定义：

        一阶差分：当自变量从  到  时， 则函数的改变量为：

        注意： 差分的自变量是x，是有序的， 离散的， 因变量是对应的值，并没有要求。差分的背景是描述自变量为时间的函数， 现实生活中很多现象都是随时间变化的。

        当自变量从x变到x+1时，函数y=y(x)一阶差分的差分称为二阶差分：

——定义（1）

         含有自变量，未知函数，差分的方程，称为差分方程。

         方程中必需含有差分，可以不包括自变量和函数。

——定义（2）

         含有未知函数几个时期下标值的方程，称为差分方程。

——定义(3)

          如果一个函数代入差分方程使两边恒等， 则称该函数为方程的解。

                    例：验证  是方程  的解

                           解：把函数代入得

                    等式两边相等，所以函数是方程的解。

——定义（4）

        差分方程的解中含有任意常数（如变量  ）, 且任意常数的个数与方程的阶数相同，则称为方程的通解。

        为了简化一下问题的形式，我们姑且只考虑单条时间序列。一个长度为T的时间序列可以被描述为

        而时间序列预测（Time Series Forecasting）则是利用历史观测的数据，去预测未来一个时间点（段）的数据。

        从统计学的角度，当我们了解了一个变量的分布函数时，我们就可以完整地描述这个变量的特征，例如正态分布：

        如果拥有多个变量，例如在上述的一个长度为T的数间序列中，那么我们则需要联合分布函数。自然，如果我们拥有了一个时间序列的所有变量的联合分布函数，我们就可以对任意一个位置的数据进行完整的统计学的预测（例如，均值，置信区间......）。

        当然这几乎是不可能的，有如下几点困难：

        OK，这么多的语句只是为了说明一下，利用严格的统计学描述进行完整的预测是显然不现实的。但很显然，我们可以把问题简化，设计出一种我们可以对分布函数进行描述并进行研究的时间序列，再利用一些手段将任意一个时间序列转化为可以研究并方便建模的时间序列，这样就可以做到合理的预测了。

         那么这种可以描述的简单时间序列就是平稳时间序列，而这所谓的一些手段就是差分方法，最后建立的模型便是今天的主角（S）ARIMA。接下来我们将会分别来进行介绍。

        时间序列的自回归模型—从线性代数的角度来看：时间序列的自回归模型—从线性代数的角度来看 - 知乎

        自回归模型（Autoregressive Model，简称 AR 模型）是最常见的平稳时间序列模型之一。

        考虑如图所示的单摆系统。设 xt 为第 t 次摆动过程中的摆幅。根据物理原理，第 t 次的摆幅 xt 由前一次的摆幅  决定，即有 。考虑到空气振动的影响，我们往往假设

        其中，随机干扰 。

        设初始时刻 x0=1，现在取不同的 a1 和 σ 值进行实验。实验结果如下图。

        我们可以看出，参数 a1 对序列的稳定性起到决定性的作用，而噪声强度  决定了序列的波动程度。

        AR(1) 模型指的是时间序列  在时间戳  时刻的取值  与时间戳  时刻的取值  相关，其公式就是：

        这个时间序列  满足如下条件：

        从 AR(1) 以上的定义出发，我们可以得到：

Proof of 1. 从 AR(1) 的模型出发，可以得到

         从而，

Proof of 2. 从 AR(1) 的模型出发，可以得到

Proof of 3. 令  ， 从  的定义出发，可以得到：

        从而，

        按照之前类似的定义，可以把 AR(1) 模型扩充到 AR(p) 模型，也就是说：

1. AR(1) 模型形如：

2. AR(2) 模型形如：

3. AR(p) 模型形如：

        AR(p) 模型的稳定性 －－－ 基于线性代数：

       对于 AR(2) 模型，可以假定  并且忽略误差项，因此可以得到简化版的模型形如：

       写成矩阵的形式形如：

        求解其特征多项式则是基于  求解可以得到  i.e。  。当  都在单位圆内部的时候，也就是该模型  满足稳定性的条件。

        对于更加一般的 AR(p) 模型，也就是考虑 p 阶差分方程

        可以用同样的方法将其转换成矩阵的形式，那就是：

        计算，  可以得到其特征多项式为：

        当每个特征值都在单位圆盘内部的时候，i.e.  该 p 阶差分方程  存在稳定性的解。

        滑动平均模型与自回归模型在形式上有一定的相似之处，其预计模型与之前项的残差有关。

        那么一个MA(q)模型可以被更加紧凑地写为:

        可以发现，该模型，使用了过去q个时期的随机干扰或预测误差来线性表达当前的预测值。

        值得注意的是这个滑动平均模型与时间序列中的滑动平均操作没啥关系。MA模型更加显式的将噪声地传递描述出来，并截断了q步以前的噪声继续由于自回归的性质传播。

        将两个模型相加，我们就获得了一个ARMA(p, q) = AR(p) + MA(q)模型，这个模型所拟合的数据通常需要一个平稳时间序列。

        自回归滑动平均模型（英语：Autoregressive moving average model，简称：ARMA模型）。是研究时间序列的重要方法，由自回归模型（简称AR模型）与移动平均模型（简称MA模型）为基础“混合”构成。在市场研究中常用于长期追踪资料的研究，如：Panel研究中，用于消费行为模式变迁研究；在零售研究中，用于具有季节变动特征的销售量、市场规模的预测等。

ARMA模型分为以下三种：

（1）自回归模型（AR：Auto-regressive）

 （2）移动平均模型（MA：Moving-Average）

（3）自回归滑动平均模型（ARMA）

        我们之前一直在讨论平稳时间序列，但是我们可以想象，在日常生活中，平稳时间序列是一个很少得到的数据，通常来讲，一个数据都拥有趋势（Trend）与季节性（Seasonality），从而让其不符合平稳时间序列的定义。但是通过差分运算，我们通常可以将一个时间序列转换为一个类平稳时间序列，从而进行ARMA的建模。我们在这一章节中先来讨论趋势（Trend），随后我们来在下一章节讨论季节性（Seasonality）。

        我们来讨论两种常见的趋势：

        第一种是多项式类型的趋势，例如线性趋势或者二次多项式趋势。

         在这里，Z_t是一个平稳时间序列，而右侧第一项则是一个k次多项式趋势。我们可以很轻松的通过差分运算消除这个趋势。差分算子的定义为：

         那么经过简单的推导我们就可以知道，一个k次多项式趋势可以被多次计算差分算子来进行抹除，只留下一个常数项（添加一个常数项不影响Z_t的平稳性）。

         第二种则是一种随机趋势，一个典型的例子便是痴汉模型（random walk model），在如下的例子中M_t便是一个痴汉模型，通过一个差分操作，我们将时间序列转化为了一个平稳时间序列。

        这种使用上一个记录直接影响下一个记录的模型，我们定义为Integrated模型。 

        那么我们已经讲述了Autoregressive Integrated Moving Average Model的所有成分，接下来我们只需要将他们加起来就行了。一个ARIMA(p,d,q)模型可以被定义为：

       其中，我们定义： 

        那么很显然，季节性是另一个可以破坏时间序列平稳性的分项，其不会被普通的差分运算所消除，同时在ARMA模型中，我们也应该加入对于周期所属位置的考虑。在附加了这两个考量之后，我们拥有了Seasonal ARIMA。

        我们可以重新定义新的季节差分算子：

         我们也可以定义AR模型与MA模型额外的季节性算子：   

        其实这两个算子并不难理解，也就是在AR模型中考虑了 ，和 MA模型中考虑了。

        最终，我们可以将SARIMA的公式写为（下划线部分为为了季节性而新添加的项）：

         通常，一个SARIMA会根据其参数表示为 

优点： 模型十分简单，只需要内生变量而不需要借助其他外生变量。

缺点： 1.要求时序数据是稳定的（stationary），或者是通过差分化(differencing)后是稳定的。 2.本质上只能捕捉线性关系，而不能捕捉非线性关系。 注意，采用ARIMA模型预测时序数据，必须是稳定的，如果不稳定的数据，是无法捕捉到规律的。比如股票数据用ARIMA无法预测的原因就是股票数据是非稳定的，常常受政策和新闻的影响而波动。

        严谨的定义： 一个时间序列的随机变量是稳定的，当且仅当它的所有统计特征都是独立于时间的（是关于时间的常量）。

判断的方法：

        稳定的数据是没有趋势(trend)，没有周期性(seasonality)的; 即它的均值，在时间轴上拥有常量的振幅，并且它的方差，在时间轴上是趋于同一个稳定的值的。

        可以使用Dickey-Fuller Test进行假设检验。

ARIMA模型有三个参数:p,d,q：

        假设一个随机过程含有d个单位根，其经过d次差分后可以变换为一个平稳的自回归移动平均过程，则该随机过程称为单积（整）自回归移动平均过程。

首先：

（1）经过d次差分后，判断该随机过程是否平稳；

（2）找到合适的d之后，xt转化为平稳的随机过程Δdxt；

（3）Δdxt构建为自回归移动平均过程，ARMA(p,q)，即完成了将随机过程xt表示为ARIMA的流程，构建好的ARIMA过程记做ARIMA(p,d,q)。p，d，q分别代表自回归阶数、差分次数、移动平均阶数。

        ARIMA模型的构建在于：寻找差分次数d；估计ARMA模型参数。差分次数d不宜过大，否则波动过大。ARMA模型的参数值通过极大似然估计参数值。

ARIMA建模流程：

        自相关函数ACF描述的是时间序列观测值与其过去的观测值之间的线性相关性。计算公式如下：

          其中k代表滞后期数，如果k=2，则代表yt和yt-2

         偏自相关函数PACF描述的是在给定中间观测值的条件下，时间序列观测值预期过去的观测值之间的线性相关性。

        举个简单的例子，假设k=3，那么我们描述的是yt和yt-3之间的相关性，但是这个相关性还受到yt-1和yt-2的影响。PACF剔除了这个影响，而ACF包含这个影响。

时间序列模型 | ARIMA - 从统计与理论层面 - 知乎

https://www.csdn.net/tags/OtDaUgxsNjE3NTMtYmxvZwO0O0OO0O0O.html